Trigonometría para poetas. El estudio de los triángulos.

La trigonometría es la rama de las matemáticas que estudia los triángulos. Muchos le temen, pero si la conocieran un poco mejor, se darían cuenta de que es más fácil de lo que se piensa.

No hace mucho me atreví a dictar una clase de trigonometría fácil por WhatsApp y no salió del todo mal. Este artículo se basa en ese ejercicio y va un poco más allá.

Qué es la trigonometría

Si comienzo diciéndote que en matemáticas, la trigonometría estudia todo tipo de triángulos, debo empezar explicándote lo básico de ángulos y triángulos, para que nos entendamos de aquí en adelante. Así que empecemos por ahí.

Qué son triángulos

Eso es mucho más fácil explicarlo con una imagen.

Como ves, son figuras geométricas que tienen tres lados, los cuales se unen en tres vértices (puntas). Los hay de diferentes tipos, pero eso te lo explico más abajo.

No se les llama tríangulos por las tres puntas, sino por los tres ángulos.

¿Ángulos? ¿Qué es eso?

Qué son ángulos

Te decía que al juntarse dos lados del triángulo se forma un vértice (punta). Pues el espacio entre los dos lados se le llama ángulo. Algunos son muy estrechos y otros muy amplios.

Los ángulos se pueden medir. Su unidad son los grados y se expresa con el símbolo °. Es el mismo símbolo que se usa para otros grados, los centígrados (°C), pero no tiene nada que ver lo uno con lo otro.

Por ejemplo, un ángulo de 45 grados se expresa 45°.

Si entiendes bien el concepto de ángulos y triángulos, ya tienes las bases de la trigonometría.

¿Para qué sirve la trigonometría?

Comienzo por completar la definición. La trigonometría es la rama de las matemáticas que te da las fórmulas para conocer la longitud de los lados y la amplitud de los ángulos en toda clase de triángulos.

En otras palabras, si tienes un triángulo y conoces algunos de sus lados o ángulos, eso te permite saberlo todo sobre ese triángulo, el tamaño de cada lado y cada ángulo.

¿Eso de qué sirve?

Ni más ni menos que te permite medir distancias a sitios a los cuales no puedes llegar. ¿No es genial?

Por ejemplo, podrías medir la altura de tu casa o la altura de la Torre Eiffel, usando tres cosas:

1. Un metro.
2. Un medidor de ángulos (se le llama transportador).
3. Una calculadora.

Te doy un ejemplo práctico. Mira la siguiente imagen.

Tú solamente puedes realizar medidas de tu lado del río, pero quieres saber qué tan ancho es. La respuesta te la da la trigonometría.

Estas son las medidas que puedes realizar.

1. La distancia entre A y B con un metro.
2. El ángulo a con el transportador.
3. El ángulo b con el transportador.

En este enlace puedes ver otros ejemplos de usos prácticos de la trigonometría.

Un poco de historia de la trigonometría.

La medición de distancias hasta lugares imposibles también la necesitaban los antiguos. Pregúntale a los Babilonios y los Egipcios hace 3.000 años.

Por ejemplo, el Faraón tendría la necesidad de saber cuál era la altura de su pirámide y si era más alta que la del faraón anterior.

¿Cómo hacían los Babilonios para saber si la Torre de Babel era la edificación más alta de la antigüedad?

Era imposible realizar esas mediciones directamente pues no tenían forma de colocar un medidor desde la cúspide hasta el suelo, atravesando la roca.

El problema en la antigüedad era que no tenían las fórmulas. Es decir, sabían que los triángulos obedecían a ciertas reglas, había una relación entre los ángulos y los lados, pero no tenían el lenguaje matemático para expresarlo en fórmulas.

Pero no se quedaron quietos. Construyeron unas tablas mediante las que hacían las aproximaciones. Era más que suficiente en su época.

Fue hasta el siglo VIII (entre 700 y 800 D.C.) cuando los árabes, con unas matemáticas más avanzadas, lograron expresar en fórmulas lo que los babilonios y egipcios ya habían descubierto.

¿Cuáles son las dichosas fórmulas?

Ellos crearon unas fórmulas generales para todo tipo de triángulos y otras para triángulos rectángulos que son una clase especial de triángulos.

Antes de darte los detalles necesito hacer un paréntesis.

Paréntesis 1: Ángulos rectos y triángulos rectángulos

Te decía que los ángulos se miden en grados. Hay unos ángulos muy especiales, y muy comunes en arquitectura. Son los ángulos rectos que miden 90° . Mira la imagen.

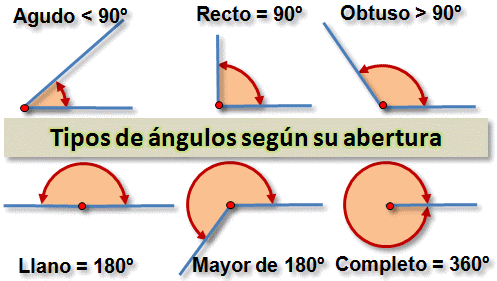
En los ángulos de 90° los dos lados son perpendiculares entre sí.

Es el mismo ángulo que forman las paredes de una casa o un edificio, con el suelo. Son perpendiculares. Si miras a tu alrededor vas a encontrar ángulos rectos en todas partes.

En tu escritorio, en la mesa del comedor, en las escaleras, en fin. A la humanidad le encantan los ángulos rectos.

En cambio, encontrar ángulos rectos en la naturaleza es mucho más difícil.

A menudo, cuando se dibujan ángulos rectos, se les señala mediante un cuadradito en la esquina para indicar que es un ángulo recto, mientras que los demás ángulos se señalan con un pequeño arco.

Y, ¿qué son los triángulos rectángulos? Sencillo. Son los que tienen un ángulo recto.

Si miras con detenimiento la primera imagen de este artículo, la de los triángulos de colores, vas a encontrar tres triángulos rectángulos. Identifícalos.

Respuesta: El verde, el rojo y el marrón.

Pero los triángulos rectángulos no son los únicos. Son seis los tipos de triángulos. Mira la imagen.

Paréntesis 2: Catetos e hipotenusa

Recuerda que los matemáticos le ponen nombre a todo. La pregunta era, ¿cómo nombrar los tres lados de un triángulo rectángulo?

La respuesta obvia de Pitágoras fue

¡Pues, catetos e hipotenusa hombre!

¿Hipo qué? Perfectamente esto habrá dicho la gente de la época cuando Pitágoras inventó el terminajo.

Entonces el asunto quedó así:

Hipotenusa. Es el lado opuesto al ángulo recto. ¿Lo recuerdas? Es el ángulo de 90 grados (90°).

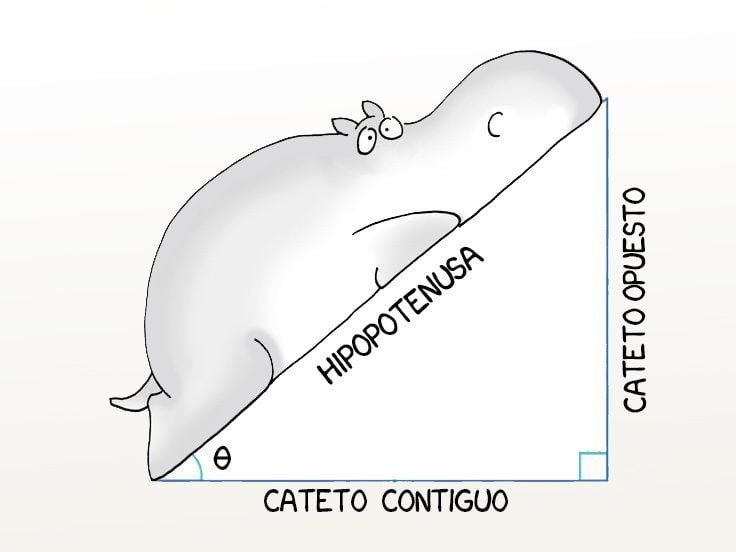
Catetos. Los dos lados que están a cada lado del ángulo recto. Pero como los matemáticos odian ponerle el mismo nombre a cosas diferentes, decidieron ponerle apellido a cada cateto. Partiendo de los ángulos sobrantes (los que no son de 90 grados) al cateto más cercano lo llamaron Cateto Adyacente (significa cercano) y Cateto Opuesto (el que está al otro lado). Mira la gráfica del hipopótamo. Al adyacente lo llaman contiguo, que significa lo mismo.

Pregunta. ¿Puede un triángulo tener dos ángulos rectos?

Respuesta. No. Si así fuera, dos de sus lados jamás se tocarían. En todo triángulo, la suma de sus ángulos es 180 grados (180°). En los triángulos rectángulos, si uno de sus ángulos es de 90°, la suma de los otros dos tiene que ser 90° también

Resumen intermedio

Hasta aquí, ya sabemos varias cosas.

1. La base de la trigonometría son ángulos y triángulos.
2. La trigonometría es la rama matemática que le pone números a los triángulos.
3. Permite determinar distancias a sitios difíciles de alcanzar.
4. Hay un caso especial con los triángulos rectángulos.
5. Los lados de los triángulos rectángulos se llaman hipotenusa y catetos.

Ahora sí estamos listos para conocer las fórmulas.

Por fin, las fórmulas de la trigonometría

Los árabes, no mucho tiempo después de la caída del Imperio Romano, descubrieron las fórmulas que gobiernan los triángulos rectángulos.

Para ello se vieron obligados a crear nuevas funciones matemáticas, a las que llamaron seno, coseno y tangente.

Esas funciones son muy importantes. Por hoy no te explicaré los detalles de lo que significan. Lo dejaremos para después. Pero sí te voy a presentar cómo lucen las dos primeras, el seno y el coseno.

Son como una ola. Como ves, sube y baja entre 1 y -1.

La función seno comienza en 0, sube hasta 1, baja hasta menos 1 (-1) y vuelve a subir hasta 0.

La función coseno luce muy parecida, con la diferencia de que comienza en 1, luego baja a 0 y sigue bajando a -1 para retornar a 0 y luego a 1.

En ambos casos, el valor oscila entre 1 y -1 siempre.

¿Y qué hay en el eje de las x (equis)? Son grados.

Al observar la gráfica podemos concluir lo siguiente de la función seno:

1. El seno de 0 grados es 0
2. El seno de 45 grados es aproximadamente 0,7
3. El seno de 90 grados es 1
4. El seno de 180 grados es 0

Trigonometría de triángulos rectángulos

La función seno, descubierta por los árabes, fue esencial para poder encontrar las fórmulas que gobiernan los triángulos rectángulos.

Esto fue lo que descubrieron.

Consejo. Las calculadoras te dan el valor seno, coseno o tangente de un ángulo. No te lo tienes que aprender.

Esas fórmulas indican, ni más ni menos, que si conoces un ángulo y un lado puedes saber todo lo demás.

Por ejemplo, si sabes que el ángulo α es de 45 grados y el valor del cateto c es 5, la fórmula sería esta:

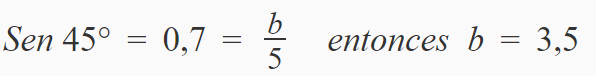
Trigonometría para todo tipo de triángulos

Para triángulos de todo tipo, los árabes descubrieron una fórmula aún más elegante. Mira esto:

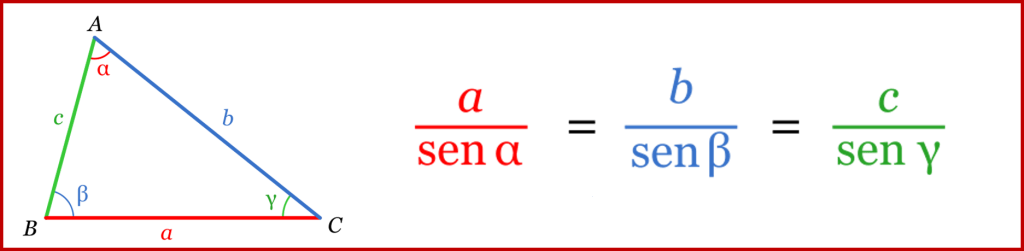
Si divides el seno de cada ángulo por el lado opuesto, vas a obtener una triple igualdad. Una fórmula perfecta.

Si tienes tres valores de un triángulo cualquiera, puedes conocer todo acerca de él.

Lo que he visto en las Pruebas SABER 11 del ICFES es que en la mayoría de los casos, las preguntas de trigonometría se enfocan en triángulos rectángulos, sin embargo, es mejor prevenir que lamentar. Estudia ambos tipos y tendrás un dominio casi total de la trigonometría.

Ejercicios de trigonometría con triángulos rectángulos.

Realiza los siguientes ejercicios para desarrollar tus habilidades con triángulos rectángulos.

Resuelve un lado de un triángulo rectángulo.

Resuelve un ángulo en triángulos rectángulos.

Problemas verbales de triángulos rectángulos.

Ejercicios de trigonometría con triángulos generales para los más PRO.

Resuelve triángulos con la ley de los senos.

Aprende qué es la ley de los cosenos y resuelve triángulos con la misma.

Problemas verbales sobre triángulos generales.

Espero que esto te haya servido un poco para desmitificar la trigonometría.

Deja abajo tus comentarios que siempre son bienvenidos.

Buen ánimo y buen genio.